Here are fifteen challenging questions for GMAT math practice, with explanations below. Can you keep the GMAT Quant pace, doing these in under 90 seconds each? As always, no calculator!
1) Let abcd be a general four-digit number and all the digits are non-zero. How many four-digits numbers abcd exist such that the four digits are all distinct and such that a + b + c = d?
(A) 6
(B) 7
(C) 24
(D) 36
(E) 42
2) Let abcd be a general four-digit number. How many odd four-digits numbers abcd exist such that the four digits are all distinct, no digit is zero, and the product of a and b is the two digit number cd?
(A) 4
(B) 6
(C) 12
(D) 24
(E) 36
3) There are 500 cars on a sales lot, all of which have either two doors or four doors. There are 165 two-door cars on the lot. There are 120 four-door cars that have a back-up camera. Eighteen percent of all the cars with back-up cameras have standard transmission. If 40% of all the cars with both back-up cameras and standard transmission are two-door cars, how many four-door cars have both back-up cameras and standard transmission?
(A) 18
(B) 27
(C) 36
(D) 45
(E) 54
4) At Mnemosyne Middle School, there are 700 students: all the students are boys or girls in the 4th or 5th grade. There are 320 students in the 4th grade, and there are 210 girls in the 5th grade. Fifty percent of the 5th graders and 40% of the 4th graders take Mandarin Chinese. Ninety 5th grade boys do not take Mandarin Chinese. The number of 4th grade girls taking Mandarin Chinese is less than half of the number of 5th grade girls taking Mandarin Chinese. Which of the following could be the number of 4th grade boys in Mandarin Chinese?
(A) 10
(B) 40
(C) 70
(D) 100
(E) 130
5) A hundred identical cubic boxes are currently arranged in four cubes: a single cubic box, a 2 x 2 x 2 cube, a 3 x 3 x 3 cube, and a 4 x 4 x 4 cube. These four are not touching each other. All outward faces are painted and all inward faces are not painted. These four cubes are going to be dismantled and reassembled as a flat 10 x 10 square. The top and all the edges of this 10 x 10 square must be painted, but there is no requirement for paint on the bottom. How many individual faces will have to be painted to accommodate the requirements of this new design?
(A) 0
(B) 5
(C) 9
(D) 16
(E) 27
6) Twelve points are spaced evenly around a circle, lettered from A to L. Let N be the total number of isosceles triangles, including equilateral triangles, that can be constructed from three of these points. A different orientation of the same lengths counts as a different triangle, because a different combination of points form the vertices. What is the value of N?
(A) 48
(B) 52
(C) 60
(D) 72
(E) 120
7) Theresa is a basketball player practicing her free throws. On her first free throw, she has a 60% chance of making the basket. If she has just made a basket on her previous throw, she has a 80% of making the next basket. If she has just failed to make a basket on her previous throw, she has a 40% of making the next basket. What is the probability that, in five throws, she will make at least four baskets?
![]()
8) Suppose a “Secret Pair” number is a four-digit number in which two adjacent digits are equal and the other two digits are not equal to either one of that pair or each other. For example, 2209 and 1600 are “Secret Pair” numbers, but 1333 or 2552 are not. How many “Secret Pair” numbers are there?
(A) 720
(B) 1440
(C) 1800
(D) 1944
(E) 2160
9) In the coordinate plane, a circle with its center on the negative x-axis has a radius of 12 units, and passes through (0, 6) and (0, – 6). What is the area of the part of this circle in the first quadrant?
![]()
10) In the coordinate plane, line L passes above the points (50, 70) and (100, 89) but below the point (80, 84). Which of the following could be the slope of line L?
(A) 0
(B) 1/2
(C) 1/4
(D) 2/5
(E) 6/7
11) At the beginning of the year, an item had a price of A. At the end of January, the price was increased by 60%. At the end of February, the new price was decreased by 60%. At the end of March, the new price was increased by 60%. At the end of April, the new price was decreased by 60%. On May 1st, the final price was approximately what percent of A?
(A) 41%
(B) 64%
(C) 100%
(D) 136%
(E) 159%
12) Suppose that, at current exchange rates, $1 (US) is equivalent to Q euros, and 1 euro is equivalent to 7Q Chinese Yuan. Suppose that K kilograms of Chinese steel, worth F Chinese Yuan per kilogram, sold to a German company that paid in euros, can be fashioned into N metal frames for chairs. These then are sold to an American company, where plastic seats & backs will be affixed to these frames. If the German company made a total net profit of P euros on this entire transaction, how much did the US company pay in dollars for each frame?
![]()
13) At the Zamenhof Language School, at least 70% of the students take English each year, at least 40% take German each year, and between 30% and 60% take Italian each year. Every student must take at least one of these three languages, and no student is allowed to take more than two languages in the same year. What is the possible percentage range for students taking both English and German in the same year?
(A) 0% to 70%
(B) 0% to 100%
(C) 10% to 70%
(D) 10% to 100%
(E) 40% to 70%
14) On any given day, the probability that Bob will have breakfast is more than 0.6. The probability that Bob will have breakfast and will have a sandwich for lunch is less than 0.5. The probability that Bob will have breakfast or will have a sandwich for lunch equals 0.7. Let P = the probability that, on any given day, Bob will have a sandwich for lunch. If all the statements are true, what possible range can be established for P?
(A) 0 < P < 0.6
(B) 0 ≤ P < 0.6
(C) 0 ≤ P ≤ 0.6
(D) 0 < P < 0.7
(E) 0 ≤ P < 0.7
![]()
(A) – 64
(B) – 7
(C) 38
(D) 88
(E) 128
Explanations for this problem are at the end of this article.
More Practice
Here are twenty-eight other articles on this blog with free GMAT Quant practice questions. Some have easy questions, some have medium, and few have quite challenging questions.
1) GMAT Geometry: Is It a Square?
2) GMAT Shortcut: Adding to the Numerator and Denominator
3) GMAT Quant: Difficult Units Digits Questions
4) GMAT Quant: Coordinate Geometry Practice Questions
5) GMAT Data Sufficiency Practice Questions on Probability
6) GMAT Quant: Practice Problems with Percents
7) GMAT Quant: Arithmetic with Inequalities
8) Difficult GMAT Counting Problems
9) Difficult Numerical Reasoning Questions
10) Challenging Coordinate Geometry Practice Questions
11) GMAT Geometry Practice Problems
12) GMAT Practice Questions with Fractions and Decimals
13) Practice Problems on Powers and Roots
14) GMAT Practice Word Problems
15) GMAT Practice Problems: Sets
16) GMAT Practice Problems: Sequences
17) GMAT Practice Problems on Motion
18) Challenging GMAT Problems with Exponents and Roots
19) GMAT Practice Problems on Coordinate Geometry
20) GMAT Practice Problems: Similar Geometry Figures
20) GMAT Practice Problems: Variables in the Answer Choices
21) Counting Practice Problems for the GMAT
22) GMAT Math: Weighted Averages
23) GMAT Data Sufficiency: More Practice Questions
24) Intro to GMAT Word Problems, Part I
25) GMAT Data Sufficiency Geometry Practice Questions
26) GMAT Data Sufficiency Logic: Tautological Questions
27) GMAT Quant: Rates and Ratios
28) Absolute Value Inequalities
Summary
These are hard problems. When you read the solutions, don’t merely read them passively. Study the strategies used, and do what you can to retain them. Learn from your mistakes!
![]()
Practice Problem Explanations
1) We need sets of three distinct integers {a, b, c} that have a sum of one-digit number d. There are seven possibilities:
- a) {1, 2, 3}, sum = 6
- b) {1, 2, 4}, sum = 7
- c) {1, 2, 5}, sum = 8
- d) {1, 3, 4}, sum = 8
- e) {1, 2, 6}, sum = 9
- f) {1, 3, 5}, sum = 9
- g) {2, 3, 4}, sum = 9
For each set, the sum-digit has to be in the one’s place, but the other three digits can be permutated in 3! = 6 ways in the other three digits. Thus, for each item on that list, there are six different possible four-digit numbers. The total number of possible four-digit numbers would be 7*6 = 42. Answer = (E)
2) The fact that abcd is odd means that cd must be an odd number and that a & b both must be odd. That limits the choices significantly. We know that neither a nor b can equal 1, because any single digit number times 1 is another single digit number, and we need a two-digit product—there are no zeros in abcd. We also know that neither a nor b can equal 5, because any odd multiple of 5 ends in 5, and we would have a repeated digit: the requirement is that all four digits be distinct.
Therefore, for possible values for a & b, we are limited to three odd digits {3, 7, 9}. We can take three different pairs, and in each pair, we can swap the order of a & b. Possibilities:
- use {3, 7}, product = 21, abcd could be 3721 or 7321
- use {3, 9}, product = 27, abcd could be 3927 or 9327
- use {7, 9}, product = 63, abcd could be 7963 or 9763
Those six are the only possibilities for abcd.
Answer = (B)
3) Total number of cars = 500
2D cars total = 165, so
4D cars total = 335
120 4D cars have BUC
“Eighteen percent of all the cars with back-up cameras have standard transmission.”
18% = 18/100 = 9/50
This means that the number of cars with BUC must be a multiple of 50.
How many 2D cars can we add to 120 4D cars to get a multiple of 50? We could add 30, or 80, or 130, but after that, we would run out of 2D cars. These leaves three possibilities for the total number with BUC:
If a total of 150 have BUC, then 18% or 27 of them also have ST.
If a total of 200 have BUC, then 18% or 36 of them also have ST.
If a total of 250 have BUC, then 18% or 45 of them also have ST.
Then we are told: “40% of all the cars with both back-up cameras and standard transmission are two-door car.”
40% = 40/100 = 2/5
This means that number of cars with both back-up cameras and standard transmission must be divisible by 5. Of the three possibilities we have, only the third words.
Total cars with BUC cams = 250 (120 with 4D and 130 with 2D)
18% or 45 of these also have ST.
40% of that is 18, the number of 2D cars with both BUC and ST.
Thus, the number of 4D cars with both BUC and ST would be
45 – 18 = 27
Answer = (B)
4) 700 student total
4G = total number of fourth graders
5G = total number of fifth graders
We are told 4G = 320, so 5G = 700 – 320 = 380
5GM, 5GF = fifth grade boys and girls, respectively
We are told 5GF = 210, so 5GM = 380 – 210 = 170
4GC, 5GC = total number of 4th or 5th graders, respectively taking Chinese
We are told
5GC = 0.5(5G) = 0.5(380) = 190
4GC = 0.4(4G) = 0.4(320) = 128
4GFM, 4GMC, 5GFC, 5GMC = 4th/5th grade boys & girls taking Chinese
We are told that, of the 170 fifth grade boys, 90 do not take Chinese, so 170 = 90 = 80 do. Thus 5GMC = 80.
5GMC + 5GFC = 5GC
80 + 5GFC = 190
5GFC = 110
We are told:
4GFM < (0.5)(5GFC)
4GFM < (0.5)(100)
4GFM < 55
Thus, 4GFM could be as low as zero or as high as 54.
4GMC = 4GC – 4GFM
If 4GFM = 0, then 4GMC = 128 – 0 = 128
If 4GFM = 54, then 4GMC = 128 – 54 = 74
Thus, fourth grade boys taking Mandarin Chinese could take on any value N, such that 74 ≤ N ≤ 128. Of the answer choices listed, the only one that works is 100.
Answer = (D)
5) The single cube has paint on all six sides. Each of the eight boxes in the 2 x 2 x 2 cube has paint on three sides (8 corner pieces). In the 3 x 3 x 3 cube, there are 8 corner pieces, 12 edge pieces (paint on two sides), 6 face pieces (paint on one side), and one interior piece (no paint). In the 4 x 4 x 4 cube, there are 8 corner pieces, 24 edge pieces, 24 face pieces, and 8 interior pieces. This chart summarizes what we have:
![]()
For the 10 x 10 flat square, we will need 4 corner pieces that have paint on three sides, 32 edge pieces that have paint on two sides (top & side), and 64 middle pieces that have paint on one side (the top).
We could use either the single total box or any of the 24 corner boxes for the four corners of the square. That leaves 21 of these, and 35 edge boxes, more than enough to cover the 32 edges of the square. The remaining ones, as well as all 30 face boxes, can be turned paint-side-up to fill in the center. The only boxes that will need to be painted, one side each, are the 9 interior boxes. Thus, we have 9 sides to paint.
Answer = (C)
6) Here’s a diagram.
![gmat math practice questions]()
First, let’s count the equilateral triangles. They are {AEI, BFJ, CGK, DHL}. There are only four of them.
Now, consider all possible isosceles triangles, excluding equilateral triangles, with point A as the vertex. We could have BAL, CAK, DAJ, and FAH. All four of those have a line of symmetry that is vertical (through A and G). Thus, we could make those same four triangles with any other point as the vertex, and we would never repeat the same triangle in the same orientation. That’s 4*12 = 48 of these triangles, plus the 4 equilaterals, is 52 total triangles.
Answer = (B)
7) There are five basic scenarios for this:
Case I: (make)(make)(make)(make)(any)
If she makes the first four, then it doesn’t matter if she makes or misses the fifth!
Case II: (miss)(make)(make)(make)(make)
Case III: (make)(miss)(make)(make)(make)
Case IV: (make)(make)(miss)(make)(make)
Case V: (make)(make)(make)(miss)(make)
Put in the probabilities:
Case I: (0.6)(0.8)(0.8)(0.8)
Case II: (0.4)(0.4)(0.8)(0.8)(0.8)
Case III: (0.6)(0.2)(0.4)(0.8)(0.8)
Case IV: (0.6)(0.8)(0.2)(0.4)(0.8)
Case V: (0.6)(0.8)(0.8)(0.2)(0.4)
Since all the answers are fractions, change all of those to fractions. Multiply the first by (5/5) so it has the same denominator as the other products.
Case I: (3/5)(4/5)(4/5)(4/5)(5/5) = 960/5^5
Case II: (2/5)(2/5)(4/5)(4/5)(4/5) = 256/5^5
Case III: (3/5)(1/5)(2/5)(4/5)(4/5) = 96/5^5
Case IV: (3/5)(4/5)(1/5)(2/5)(4/5) = 96/5^5
Case V: (3/5)(4/5)(4/5)(1/5)(2/5) = 96/5^5
Add the numerators. Since 96 = 100 – 4, 3*96 = 3(100 – 4) = 300 – 12 = 288.
288 + 256 + 960 = 1504
P = 1504/5^5
Answer = (E)
8) There are three cases: AABC, ABBC, and ABCC.
In case I, AABC, there are nine choices for A (because A can’t be zero), then 9 for B, then 8 for C. 9*9*8 = 81*8 = 648.
In case II, ABBC, there are 9 choices for A, 9 for B, and 8 for C. Again, 648.
In case III, ABCC, there are 9 choices for A, 9 for B, and 8 for C. Again, 648.
48*3 = (50 – 2)*3 = 150 – 6 = 144
3*648 = 3(600 + 48) = 1800 + 144 = 1948
Answer = (D)
9)
![]()
We know that the distance from A (0,6) to B (0, – 6) is 12, so triangle ABO is equilateral. This means that angle AOB is 60°. The entire circle has an area of
![]()
A 60° angle is 1/6 of the circle, so the area of sector AOB (the “slice of pizza” shape) is
![]()
The area of an equilateral triangle with side s is
![]()
Equilateral triangle AOB has s = 12, so the area is
![]()
If we subtract the equilateral triangle from the sector, we get everything to the right of the x-axis.
![]()
Again, that’s everything to the right of the x-axis, the parts of the circle that lie in Quadrants I & IV. We just want the part in Quadrant I, which would be exactly half of this.
![]()
Answer = (C)
10) One point is (50, 70) and one is (100, 89): the line has to pass above both of those. Well, round the second up to (100, 90)—if the line goes above (100, 90), then it definitely goes about (100, 89)!
What is the slope from (50, 70) to (100, 90)? Well, the rise is 90 – 70 = 20, and the run is 100 – 50 = 50, so the slope is rise/run = 20/50 = 2/5. A line with a slope of 2/5 could pass just above these points.
Now, what about the third point? For the sake of argument, let’s say that the line has a slope of 2/5 and goes through the point (50, 71), so it will pass above both of the first two points. Now, move over 5, up 2: it would go through (55, 73), then (60, 75), then (65, 77), then (70, 79), then (75, 81), then (80, 83). This means it would pass under the third point, (80, 84). A slope of 2/5 works for all three points.
We don’t have to do all the calculations, but none of the other slope values works.
Answer = (D)
11) The trap answer is 100%: a percent increase and percent decrease by the same percent do not cancel out.
Let’s say that the A = $100 at the beginning of the year.
End of January, 60% increase. New price = $160
End of February, 60% decrease: that’s a decrease of 60% of $160, so that only 40% of $160 is left.
10% of $160 = $16
40% of $160 = 4(16) = $64
That’s the price at the end of February.
End of March, a 60% increase: that’s a increase of 60% of $64.
10% of $64 = $6.40
60% of $64 = 6(6 + .40) = 36 + 2.4 = $38.40
Add that to the starting amount, $64:
New price = $64 + $38.40 = $102.40
End of April, 60% decrease: that’s a decrease of 60% of $102.40, so that only 40% of $102.40 is left.
At this point, we are going to approximate a bit. Approximate $102.40 as $100, so 40% of that would be $40. The final price will be slightly more than $40.
Well, what is slightly more than $40, as a percent of the beginning of the year price of $100? That would be slightly more than 40%.
Answer = (A)
12) The K kilograms, worth F Chinese Yuan per kilogram, are worth a total of KF Chinese Yuan. The German company must pay this amount.
Since 1 euro = (7Q) Chinese Yuan, then (1/(7Q)) euro = 1 Chinese Yuan, and (KF/7Q) euros = KF Chinese Yuan. That’s the amount that the Germans pay to the Chinese.
![]()
That is the German company’s outlay, in euros. Now, they make N metal chairs, and sell them, making a gross profit of P euros.
![]()
That must be the total revenue of the German company, in euros. This comes from the sale to the American company. Since $1 = Q euros, $(1/Q) = 1 euro, so we change that entire revenue expression to euros to dollars, we divide all terms by Q.
![]()
That must be the total dollar amount that leaves the American company and goes to the German company. This comes from the sale of N metal frames for chairs, so each one must have been 1/N of that amount.
![]()
Answer = (A)
13) First, we will focus on the least, the lowest value. Suppose the minimum of 70% take English, and the minimum of 40% take German. Even if all 30% of the people not taking English take German, that still leaves another 10% of people taking German who also have to be taking English. Thus, 10% is the minimum of this region.
Now, the maximum. Both the German and English percents are “at least” percents, so either could be cranked up to 100%. The trouble is, though, that both can’t be 100%, because some folks have to take Italian, and nobody can take three languages at once. The minimum taking Italian is 30%. Let’s assume all 100% take German, and that everyone not taking Italian is taking English: that’s 70% taking English, all of whom also would be taking German. Thus, 70% is the maximum of this region.
Answer = (C)
14) Let A = Bob eats breakfast, and B = Bob has a sandwich for lunch. The problem tells us that:
P(A) > 0.6
P(A and B) < 0.5
P(A or B) = 0.7
First, let’s establish the minimum value. If Bob never has a sandwich for lunch, P(B) = 0, then it could be that P(A and B) = 0, which is less than 0.5, and it could be that P(A) = 0.7, which is more than 0.6, so that P(A or B) = 0.7. All the requirements can be satisfied if P(B) = 0, so it’s possible to equal that minimum value.
Now, the maximum value. Since P(A or B) = 0.7, both P(A) and P(B) must be contained in this region. See the conceptual diagram.
![]()
The top line, 1, is the entire probability space. The second line, P(A or B) = 0.7, fixes the boundaries for A and B. P(A) is the purple arrow, extending from the right. P(B) is the green arrow extending from the left. The bottom line, P(A and B) < 0.5, is the constraint on their possible overlap.
Let’s say that P(A) is just slightly more than 0.6. That means the region outside of P(A), but inside of P(A or B) is slightly less than 1. That’s the part of P(B) that doesn’t overlap with P(A). Then, the overlap has to be less than 0.5. If we add something less than 1 to something less than 5, we get something less than 6. P(B) can’t equal 0.6, but it can any value arbitrarily close to 0.6.
Thus, 0 ≤ P(B) < 0.6.
Answer = (B)
15)
![]()
Answer = (E)
The post Challenging GMAT Math Practice Questions appeared first on Magoosh GMAT Blog.







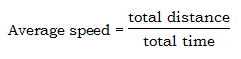
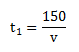
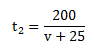

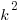 . That is BIG IDEA #2 of this post.
. That is BIG IDEA #2 of this post. — that means area goes up to 225 percent, which is an increase of 125% above the original 100%. Thus, area would increase by 125%.
— that means area goes up to 225 percent, which is an increase of 125% above the original 100%. Thus, area would increase by 125%. . That is BIG IDEA #3 of this post.
. That is BIG IDEA #3 of this post. . If each side of a box is multiplied by 5, k = 5, then the total volume is multiplied by
. If each side of a box is multiplied by 5, k = 5, then the total volume is multiplied by  .
. , which is the multiplier for a 44% increase. That’s the percent increase in area. Answer = D
, which is the multiplier for a 44% increase. That’s the percent increase in area. Answer = D , which is the multiplier for a 96% increase. That’s the percent increase in area. Answer = E
, which is the multiplier for a 96% increase. That’s the percent increase in area. Answer = E approximately. That would be the multiplier for a 94% decrease, because 1 – 0.94 = 0.06; therefore, the volume decreases by 94%. Answer = E.
approximately. That would be the multiplier for a 94% decrease, because 1 – 0.94 = 0.06; therefore, the volume decreases by 94%. Answer = E.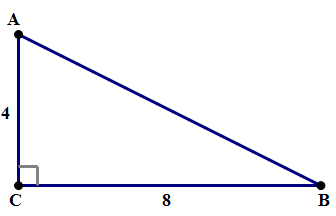
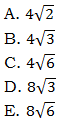
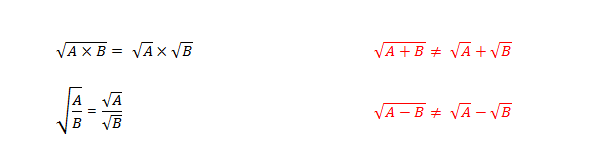
 , which means writing it as a product of some positive integer and some much smaller root. In order to do this, we are going to use the first property given in the previous section: we can separate the square-root by multiplication. The trick is: for 72, find any factor which is a perfect square. For example,
, which means writing it as a product of some positive integer and some much smaller root. In order to do this, we are going to use the first property given in the previous section: we can separate the square-root by multiplication. The trick is: for 72, find any factor which is a perfect square. For example,  , and 9 is a perfect square. Therefore
, and 9 is a perfect square. Therefore
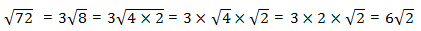
 . Then:
. Then: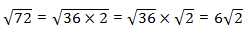

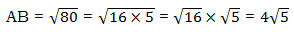

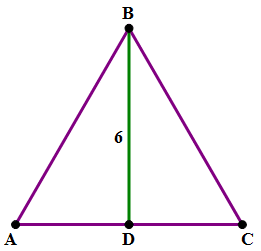
 . Let’s not simplify that, but just leave that as is. You see, we are going to use the Pythagorean Theorem again, in the right triangle ACD, so even if we found out the square-root of s, we would have to turn around and square it again anyway.
. Let’s not simplify that, but just leave that as is. You see, we are going to use the Pythagorean Theorem again, in the right triangle ACD, so even if we found out the square-root of s, we would have to turn around and square it again anyway.
 .
.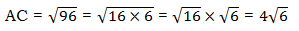


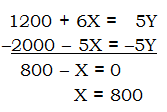






 , and
, and  are all terms. When we add terms together, we get a polynomial. A polynomial with two terms is a binomial. For example,
are all terms. When we add terms together, we get a polynomial. A polynomial with two terms is a binomial. For example,  ,
,  , and
, and  are all binomials. A polynomial with three terms is a trinomial. In the question above, each of the five answer choices is a trinomial.
are all binomials. A polynomial with three terms is a trinomial. In the question above, each of the five answer choices is a trinomial. . Here is a step-by-step guide to the FOIL process for this.
. Here is a step-by-step guide to the FOIL process for this.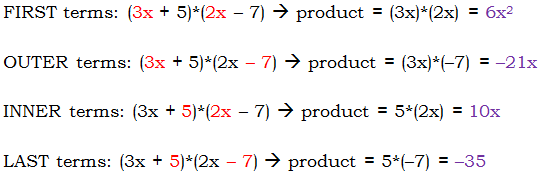




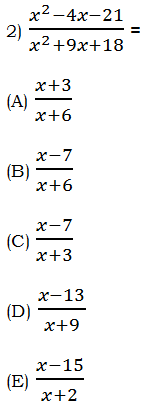
 , then |a| + |b| + |c| + |d| =
, then |a| + |b| + |c| + |d| =
 , then to factor it, we are looking for two numbers that have a product of c and a sum of b.
, then to factor it, we are looking for two numbers that have a product of c and a sum of b.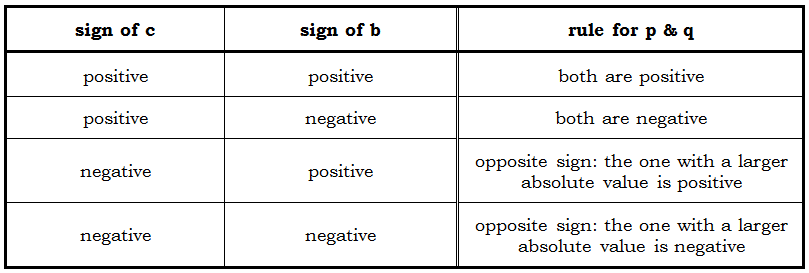
 . Since c = –18 is negative, that means the p & q we want will have opposite sign: one positive, one negative. Since b = –7 is also negative, that means which one, p or q, has the larger absolute value, that one will be negative. We are looking for a bigger negative, and smaller positive, which will have a product of –18 and a sum of –7. One way to think about this is: we need a pair of factors of 18 that have a difference of 7. These two numbers are clearly 9 & 2. Make the bigger one negative: –9 & +2. Those are the numbers we need. Now, stick these into the factoring format:
. Since c = –18 is negative, that means the p & q we want will have opposite sign: one positive, one negative. Since b = –7 is also negative, that means which one, p or q, has the larger absolute value, that one will be negative. We are looking for a bigger negative, and smaller positive, which will have a product of –18 and a sum of –7. One way to think about this is: we need a pair of factors of 18 that have a difference of 7. These two numbers are clearly 9 & 2. Make the bigger one negative: –9 & +2. Those are the numbers we need. Now, stick these into the factoring format:
 . This is tricky, because you are looking for four integers: a, b, c, and d, such that
. This is tricky, because you are looking for four integers: a, b, c, and d, such that  . The constraints we have are
. The constraints we have are




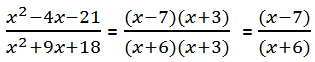



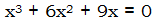



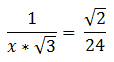

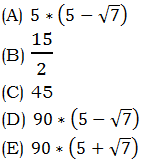


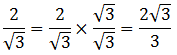
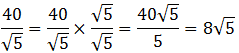
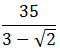
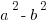 = (a + b)(a – b). Factors of the form (a + b) and (a – b) are called conjugates of one another. When we have (number + square root) in the denominator, we create the conjugate of the denominator by changing the addition sign to a subtraction sign, and then multiply both the numerator and the denominator
= (a + b)(a – b). Factors of the form (a + b) and (a – b) are called conjugates of one another. When we have (number + square root) in the denominator, we create the conjugate of the denominator by changing the addition sign to a subtraction sign, and then multiply both the numerator and the denominator 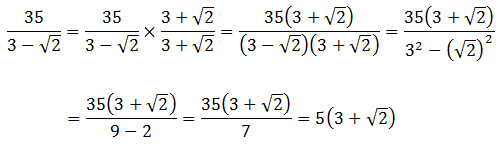


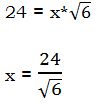
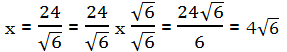
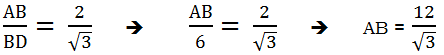
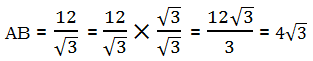
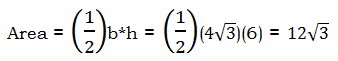
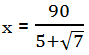
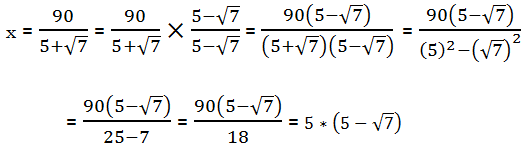
 , then what is the value of
, then what is the value of  ?
? = 7
= 7







 = X – 17. In other words, if we could find the value of
= X – 17. In other words, if we could find the value of 


 . For that we need the radius, OC. We are not given this directly, but notice that r = OC = DC – OD = a – b. If we knew that, we could find the area of the circle.
. For that we need the radius, OC. We are not given this directly, but notice that r = OC = DC – OD = a – b. If we knew that, we could find the area of the circle.
 , so we just have to multiply by pi and we have the area. This statement, alone and by itself, is sufficient.
, so we just have to multiply by pi and we have the area. This statement, alone and by itself, is sufficient.













 . What is the value of
. What is the value of  ?
? . Therefore
. Therefore  . Because the question has two apostrophe signs, we want to repeat this procedure to get,
. Because the question has two apostrophe signs, we want to repeat this procedure to get,  . Answer (D).
. Answer (D). . What the value of p in
. What the value of p in  ?
? . Solving for p:
. Solving for p:
 .
. . How many unique sums of x and y result, if x@y is an integer less than 15?
. How many unique sums of x and y result, if x@y is an integer less than 15?![[[-pi]] + [[-sqrt{37}]] [[-pi]] + [[-sqrt{37}]]](http://magoosh.com/gmat/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_7a5a4d0aa93936c2196319655062a142.png) ?
?![[[9.4]] [[9.4]]](http://magoosh.com/gmat/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_271600f6fef0554fae383a4dbcb3ad1b.png)
![[[4 pi]] [[4 pi]]](http://magoosh.com/gmat/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_b909ac5f9836c7d88e831789c215b486.png)
![[[sqrt{99}]] [[sqrt{99}]]](http://magoosh.com/gmat/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_5c6704c56088e290c28b4273cc6c0881.png)
![[[sqrt{120}]] [[sqrt{120}]]](http://magoosh.com/gmat/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_c04dba42e4ebbafc5536adbdf7cf4c6d.png)
![[[sqrt{143}]] [[sqrt{143}]]](http://magoosh.com/gmat/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_eccd8678d22d160d7619da4672cc55c9.png)
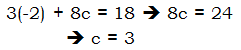
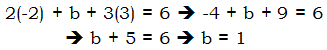
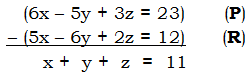



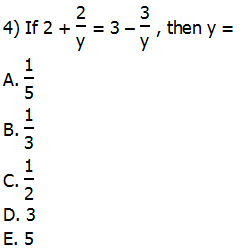



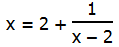

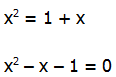
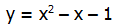
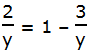
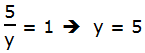











 = (a + b)(a – b). Los factores de la forma (a + b) y (a – b) se llaman conjugados entre sí. Cuando tenemos (número + raíz cuadrada) en el denominador, creamos el conjugado del denominador cambiando el signo de suma a un signo de resta, y luego multiplicamos tanto el numerador como el denominador por el conjugado del denominador. En el ejemplo anterior, el denominador es tres menos la raíz cuadrada de dos. El conjugado del denominador sería tres más la raíz cuadrada de dos. Para racionalizar el denominador, multiplicamos tanto el numerador como el denominador por este conjugado.
= (a + b)(a – b). Los factores de la forma (a + b) y (a – b) se llaman conjugados entre sí. Cuando tenemos (número + raíz cuadrada) en el denominador, creamos el conjugado del denominador cambiando el signo de suma a un signo de resta, y luego multiplicamos tanto el numerador como el denominador por el conjugado del denominador. En el ejemplo anterior, el denominador es tres menos la raíz cuadrada de dos. El conjugado del denominador sería tres más la raíz cuadrada de dos. Para racionalizar el denominador, multiplicamos tanto el numerador como el denominador por este conjugado.

































